Yes. We are to claim the irrationality of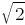 
.
We will use proof by contradiction.
Assume that 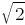is a rational number. Then by definition of rational numbers, we may write that
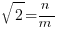
where n, m are integers.
Squaring on both sides: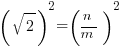 
, or
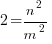
which leads to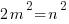 
(*)
Let us show that (*) cannot hold true.
Method 1.
Let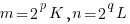 
, where p, q are integers, K and L are odd integers.
{If either K or L are even numbers, then factor 2 can be extracted iteratively until an odd number (co-factor) is revealed. }
Bringing m, n in the above forms into 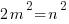, then:
(++)
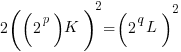
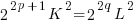Let us count the number of 2’s on each side. The l.h.s has (2p+1) of factor 2’s (an odd count of 2), and the r.h.s. has (2q) of 2’s (an even count of 2’s). However, it is well established that for any integer, the prime factorization is unique. Therefore, equation (++) cannot holds. Tracing back, we have to revoke the initial assumption
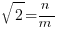
Therefore, number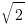 
is not a rational number.
Method 2.
Note in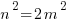 
, the right hand side is even, so the left side is also even. This implies that n must contain factor 2. Let n = 2 N, then
— > 
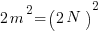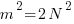
where the new equation 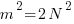implies that number m must contain factor 2. So each of n, m and N contains factor 2.
This process may be applied in an iterative manner, forever. Consequently, both m and n contains an infinite many factors of 2’s. However, this is not possible as either n or m is a finite number.
You got it?
If you got it, you shall be able to prove that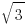 
is also irrational (i.e. 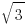cannot be written as the ratio of two integers.) How? Just use the same idea, but this time, you need to count the number of 3’s.
