下图中,ABC是直角三角形;C是直角。如图所示是勾股定理的一个证明。您看明白了吗?
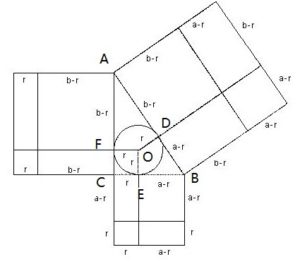
耐人寻味的是这里用到了直角三角形的内切圆,与三边(两直角边和一斜边)分别相切于三点 D,E,F。过这三个切点的半径把圆分成三部分。而每一部分都是对称的!由此首先:
c = (a-r) + (b-r) = a+b – 2r
其中 c 是斜边长,a, b 是两直角边长,r 是这内切圆的半径。
我们于是有
c2 = (a-r + b-r)2
为证勾股定理,余下的就是把上式的右边变化成 a2 + b2. 建立的方法是通过切割面积c2 利用面积相等把切割的小块与 a2 + b2 中的小块完全匹配。(记 O 是内切圆的中心. 注意 D,E,F 是三个切点。)
看一眼如下的推演:
c2 = (a+b-2r)2
c2 = (a+b)2 – 4r (a+b) + 4 r2
c2 = a2 + b2 + 2ab – 4r (a+b-r)
在上面式子中,划掉尾巴上的两项,就是勾股定理。所以我们只要证明:
2 ab = 4r (a+b-r)
即(ab)/2= r (a+b-r). 注意!直角三角形的面积是啥?是 (ab/2). 直角三角形ABC(被过三切点的半径)分成三块:四边形 OFAD,ODBE 还有OECF(正方形):面积分别是 r (b-r), r(a-r), 还有 r2. 加起来,ABC 的总面积不就是 r(a+b-r) ?由此(ab) /2 = r (a+b-r).
之所以说内切圆的使用耐人寻味,是因为在本证明中只是利用切点去分割三角形;割成的三小块:四边形 OFAD,ODBE 还有OECF(正方形)面积都与 r 有关。是不是很有趣?
啊哈! 证明毕。