Let us start from rational numbers. If one wants to test whether a given number is rational, then he/she will attempt to write it as the ratio of two integers – this is conceptually applicable. To elaborate, if a number is already in this form, of course it is rational. But to claim the opposite is not that straight forward. How would you show that 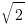 (or
(or 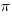 ) is irrational? There are infinitely many integers, so the ratios of two integers are infinitely many; if you just show an irrational number does not equal to many such ratios numerically, you made little progress in showing it is irrational.
) is irrational? There are infinitely many integers, so the ratios of two integers are infinitely many; if you just show an irrational number does not equal to many such ratios numerically, you made little progress in showing it is irrational.
In mathematics, if one is given an approximate value, then it does not make sense to ask whether the given value is rational or not. The reason is, there are infinitely many rational numbers that are so close to an irrational number (more strictly, we can construct a sequence of rational numbers which converge to, or has limit, to be the given irrational number). For example, consider 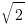
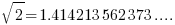
and the sequence
{1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, .. .. .. }
and the sequence
{2, 1.5, 1.42, 1.415, 1.4143, 1.41422, 1.414214, .. .. .. }
Of the above two sequences, each has the limit as 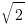 – which implies you cannot isolate an interval on the real axis to claim, all within that interval are irrational numbers. Between two irrational numbers, there are (infinitely) many rational numbers.
– which implies you cannot isolate an interval on the real axis to claim, all within that interval are irrational numbers. Between two irrational numbers, there are (infinitely) many rational numbers.
To make it meaningful to ask whether a number is irrational, it must be given in an exact form – two of such forms are radical numbers (like 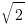 ), or an expression that involve well known constant(s), e.g.
), or an expression that involve well known constant(s), e.g. 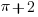 , where
, where 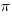 is the ratio (of a circle): DEFINED as the ratio of circumference to diameter. There are three simple rules that we can resort to for deciding whether a number given (in exact form) is irrational or not, as:
is the ratio (of a circle): DEFINED as the ratio of circumference to diameter. There are three simple rules that we can resort to for deciding whether a number given (in exact form) is irrational or not, as:
(a) The square root of a non perfect-square number is always an irrational number;
Or: if the square root of an integer is not an integer, then it must be an irrational number.
Example: 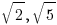
(b) An irrational number added to (subtracted from) a rational number, or multiplied by (divided by) a rational number (the multiplier or divisor is not 0), will always result in an irrational number.
Example: 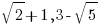
(c) If an arithmetic expression (only add/subtract/multiply/division) involves any count of rational numbers but only one irrational, and that irrational is not reduced to zero by a zero multiplier, then the result will always be an irrational number.
Example: 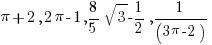
If we are given a number that is not directly in any of the forms (i) (ii) (iii), then to use these rules, we will have to do some work: try simplifying the given expression while keeping the exact value.
Rule (a) shall be extended (as we shall consider the cubic root, fourth power root etc.) as: for a power root of n-th exponent (n is any integer), if the radicand is not a perfect n-th power number, then the result of this power root must be an irrational number. For example, 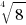 is an irrational number (since 8 is not a perfect 4-th power number).
is an irrational number (since 8 is not a perfect 4-th power number).
To appreciate those rules, let us attempt the question below. Of the following numbers, which is a rational number, and which is an irrational number?
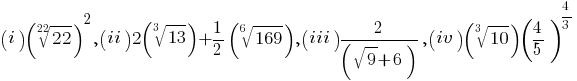
If you forget the definition of fraction exponent, you may want to quickly review for it. The key to the above question is: among the four numbers listed as (i) (ii) (iii) (iv):
- (i) (ii) are irrational numbers:
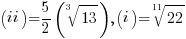 ;
;
- (iii) (iv) are rational numbers:
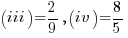 .
.
Suppose an expression results in a rational number. Only a slight change will bring it to an irrational number. For example, 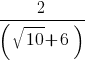 is an irrational number (since the square root of 10 is irrational, which adds to 6 to get a sum, then take reciprocal and then double). See how similar the form is to the given form (iii) !
is an irrational number (since the square root of 10 is irrational, which adds to 6 to get a sum, then take reciprocal and then double). See how similar the form is to the given form (iii) !
In the next post, for the first rule — rule (a) — an example (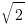 ) will be shown strictly as an irrational number (we not only know that rule, but also try to understand why the rule stands true).
) will be shown strictly as an irrational number (we not only know that rule, but also try to understand why the rule stands true).
Meanwhile, we note the constant 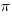 is defined as a ratio (checking up the definition – if you want), and we say it is an irrational number. Why so? Find the explanation in the next post.
is defined as a ratio (checking up the definition – if you want), and we say it is an irrational number. Why so? Find the explanation in the next post.
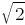 .
.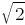 is a rational number. Then by definition of rational numbers, we may write that
is a rational number. Then by definition of rational numbers, we may write that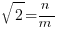
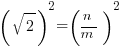 , or
, or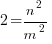
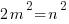 (*)
(*)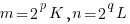 , where p, q are integers, K and L are odd integers.
, where p, q are integers, K and L are odd integers. 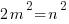 , then:
, then: 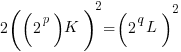
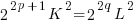 (++)
(++)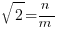
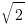 is not a rational number.
is not a rational number.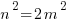 , the right hand side is even, so the left side is also even. This implies that n must contain factor 2. Let n = 2 N, then
, the right hand side is even, so the left side is also even. This implies that n must contain factor 2. Let n = 2 N, then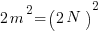 — >
— > 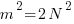
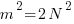 implies that number m must contain factor 2. So each of n, m and N contains factor 2.
implies that number m must contain factor 2. So each of n, m and N contains factor 2. 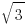 is also irrational (i.e.
is also irrational (i.e. 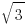 cannot be written as the ratio of two integers.) How? Just use the same idea, but this time, you need to count the number of 3’s.
cannot be written as the ratio of two integers.) How? Just use the same idea, but this time, you need to count the number of 3’s.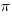 ) is irrational? There are infinitely many integers, so the ratios of two integers are infinitely many; if you just show an irrational number does not equal to many such ratios numerically, you made little progress in showing it is irrational.
) is irrational? There are infinitely many integers, so the ratios of two integers are infinitely many; if you just show an irrational number does not equal to many such ratios numerically, you made little progress in showing it is irrational.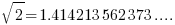
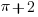 , where
, where 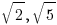
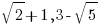
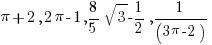
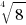 is an irrational number (since 8 is not a perfect 4-th power number).
is an irrational number (since 8 is not a perfect 4-th power number). 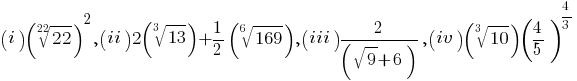
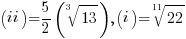 ;
; 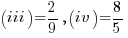 .
.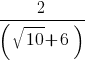 is an irrational number (since the square root of 10 is irrational, which adds to 6 to get a sum, then take reciprocal and then double). See how similar the form is to the given form (iii) !
is an irrational number (since the square root of 10 is irrational, which adds to 6 to get a sum, then take reciprocal and then double). See how similar the form is to the given form (iii) !